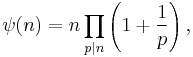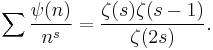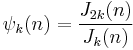Dedekind psi function

In number theory, the Dedekind psi function is the multiplicative function on the positive integers defined by

$\psi(n) = n \prod_{p|n}\left(1%2B\frac{1}{p}\right),$

where the product is taken over all primes p dividing n (by convention, ψ(1) is the empty product and so has value 1). The function was introduced by Richard Dedekind in connection with modular functions.

The value of ψ(n) for the first few integers n is:

1, 3, 4, 6, 6, 12, 8, 12, 12, 18, 12, 24 ... (sequence A001615 in OEIS).

ψ(n) is greater than n for all n greater than 1, and is even for all n greater than 2. If n is a square-free number then ψ(n) = σ(n).

The ψ function can also be defined by setting ψ(pⁿ) = (p+1)p^n-1 for powers of any prime p, and then extending the definition to all integers by multiplicitivity. This also leads to a proof of the generating function in terms of the Riemann zeta function, which is

$\sum \frac{\psi(n)}{n^s} = \frac{\zeta(s) \zeta(s-1)}{\zeta(2s)}.$

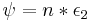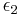This is also a consequence of the fact that we can write as a Dirichlet convolution of $\psi= n * \epsilon_2$ where $\epsilon_2$ is the characteristic function of the squares.

Higher Orders

The generalization to higher orders via ratios of Jordan's totient is

$\psi_k(n)=\frac{J_{2k}(n)}{J_k(n)}$

with Dirichlet series

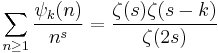$\sum_{n\ge 1}\frac{\psi_k(n)}{n^s} = \frac{\zeta(s)\zeta(s-k)}{\zeta(2s)}$ .

It is also the Dirichlet convolution of a power and the square of the Mobius function,

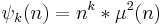$\psi_k(n) = n^k * \mu^2(n)$ .

$\epsilon_2 = 1,0,0,1,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0\ldots$

is the characteristic function of the squares, another Dirichlet convolution leads to the generalized σ-function,

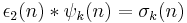$\epsilon_2(n) * \psi_k(n) = \sigma_k(n)$ .

References

Goro Shimura, Introduction to the Arithmetic Theory of Automorphic Functions, Princeton, 1971 (page 25, equation (1))
Mathar, Richard J. (2011). "Survey of Dirichlet series of multiplicative arithmetic functions". arXiv:1106.4038. Section 3.13.2
A065958 is ψ₂, A065959 is ψ₃, and A065960 is ψ₄
Carella, N. A. (2010). "Squarefree Integers And Extreme Values Of Some Arithmetic Functions". arXiv:1012.4817v3.

External links

Weisstein, Eric W., "Dedekind Function" from MathWorld.